Van used coaxial delay lines in his two-element phased array, and some users still use delay lines with good results.  However, we must always remember this extremely important fact about delay lines….. 

The phase shift of a transmission line is only equal to its electrical length when the line is terminated into its characteristic impedance.

What is the statistical probability that the feedpoint impedance at either element of a two-element phased array will be the characteristic impedance of coax, 50 + j0?  I am inclined to think that your chances of winning the lottery is better than the chance of finding a purely resistive 50 ohm load at either element of a two-element phased array.  Delay line proponents assume they are cutting a line of a particular electrical length, but in practice the electrical length of their line depends upon the impedance of the load it is terminated in.

Another compromise of using delay lines is that the delay line has no flexibility to perform impedance matching that will cause equal current magnitudes to flow into each element.  Equal currents in each element are required for maximum front-to-back. Unfortunately, delay lines fall far short of providing the ability to simultaneously achieve optimal phase shift and optimal impedance matching that is required for equal currents in each element.

The variable LC phasing network, however, does give the flexibility of achieving optimal phase shift and optimal impedance matching for optimal current distribution.

Figure 1 below is a sketch of the simple two-component LC phasing network that I used for years with the phased array. 

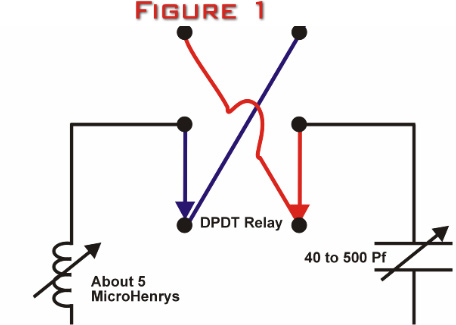
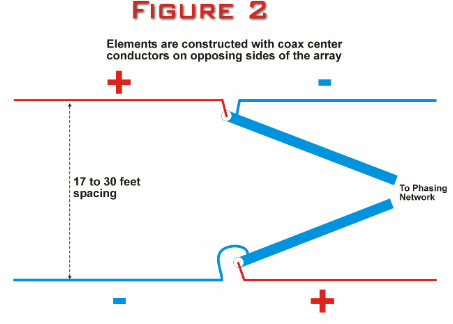
Figure 2 below illustrates the feedline connections to the elements.  Please notice there is a 180 degree phase reversal by putting the shields on opposite sides of the array.  Some users get best results without transposing the feedlines, but I have always found the nulls easier to identify with the feedlines transposed. 

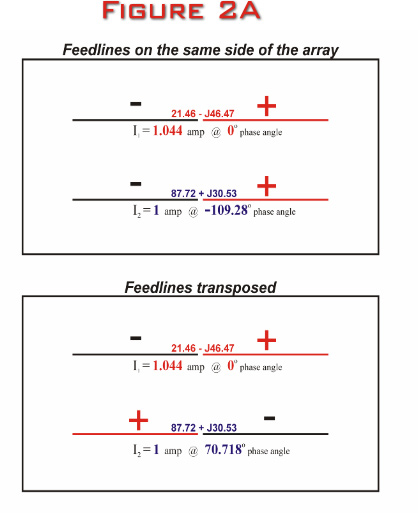
Figure 2A below illustrates both the transposed and non-transposed configurations of the array, along with the feedpoint impedances, current amplitudes and current phase relationships.  Please notice that all parameters are identical for both configurations at maximum front-to-back, except for the current phase relationships. 

Figure 2B below illustrates why the two configurations are really identical.  The difference in phase relationship between the transposed and non-transposed configurations is +70.718 – (-109.28) degrees, which is equal to 180 degrees, the exact additional phase shift created by transposing the feedlines.  The reason I transpose my feedlines is that it is easier to create the +70 degrees of phase shift with the LC network for the transposed configuration than it is to create the –109 degrees with the LC network for the non-transposed configuration.

When adjusting the array for maximum front-to-back, the roller coil and variable capacitor are adjusted for a signal null.  Although this works well, the roller coil changes reactance relatively slowly as compared to sweeping a variable capacitor through its range of reactance.  This makes identifying the deepest part of the signal null difficult as the roller inductor is turned back and forth.  After twenty years of using the two-component LC network, it finally dawned on me that the addition of a variable capacitor in series with the roller coil would make it much easier to identify the null in the inductive leg by utilizing more coil (inductive reactance) than necessary, and then adding a series variable capacitor (capacitive reactance).  By tuning the variable capacitor in series with the roller coil, I could sweep rapidly through a wide range of net inductive reactance values to identify the maximum front-to-back null.  By choosing a value of the fixed inductance carefully, the values of the variable capacitor can be determined that will allow the net reactance of the inductive leg to remain inductive over the majority of the capacitive values.  The great advantage of this three-component LC network is tuning speed in the inductive leg.  And so was born the three- component L/C phasing network, illustrated by the sketch in Figure 3 below.

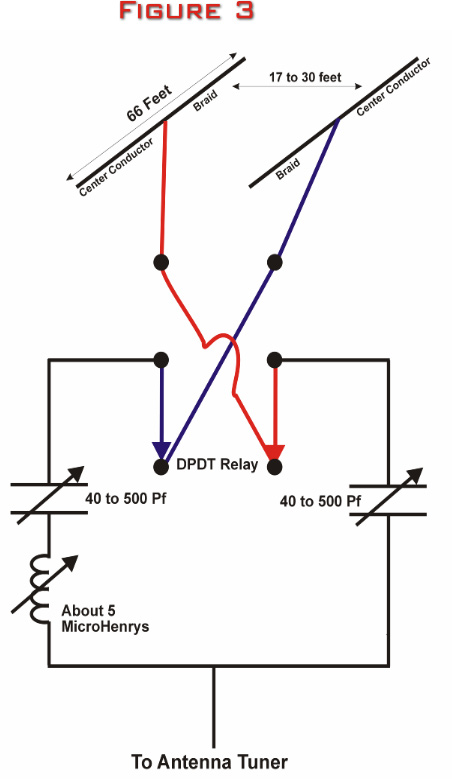
The three-component L/C phasing network (Photograph in Figure 4 below) is extremely quick to find the null and is very precise.  Amateur radio operators are already accustomed to using two hands with the tune and load knobs to adjust their power amplifiers, so the neural pathways are already established to adjust the two capacitors of the three-component LC phasing network to identify maximum front-to-back.

Figure 5 below shows the reactance of the capacitor in the capacitive leg as it is swept through it’s range of values. 

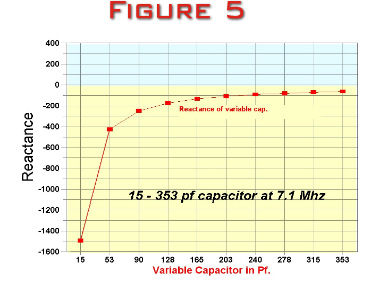
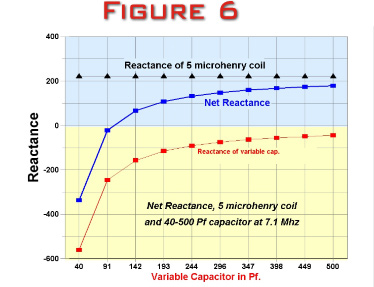
Figure 6 below illustrates the net reactance of the series coil/capacitor combination in the inductive leg as the capacitor is swept though it’s range of values. Please note that the two capacitors must be isolated above ground on ceramic standoff insulators.  The roller coil is typically isolated above ground by its housing, but if in doubt, put it on ceramic standoff insulators also.  I used vacuum relays for the switching, but a conventional DPDT RF relay works just as well.  I have even used a Radio Shack knife switch for the switching and it also worked well.

When sifting through the antenna literature, one immediately recognizes the similarity of this antenna to the famous "8JK" by John Kraus, W8JK.  The “8JK” is bi-directional because of the 180 degree phasing between its elements.  The two-element phased array as described in these pages is unidirectional and has a typical horizontal pattern very much like the parasitic yagi.  The phase relationship between the elements for maximum cancellation is somewhere between 115 to 150 degrees, depending upon the spacing between the elements, the height above ground, and the arrival angle of the incoming signal.